As you may recall, we had a little curiosity arise concerning oblique asymptotes. Specifically, how does the function behave if the difference in degree with respect to the numerator and denominator is greater than one? Is an asymptote defined by a nonlinear quotient after performing long division? It seems that this would be a natural consequence imposed by the definition of an oblique asymptote. In essence what I am asking is whether or not it is possible to have a nonlinear curve which defines an asymptote. Why not? I did some preliminary test with some easy cases and I think you may find the results interesting. It seems that these functions do indeed behave asymptotically around these quadratic and cubic quotients.

I considered the following two equations,

The equivalent expression after the equality statement is derived after performing long division. It is important here to notice the quotients of each of these expression as they are the functions we claim will behave as asymptotes. The quotients are,

and,

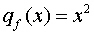
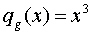
Now I will use the definition of an oblique asymptote given in the book to show that for large values of x the distance between g(x) and its quotient are small.

Indeed,

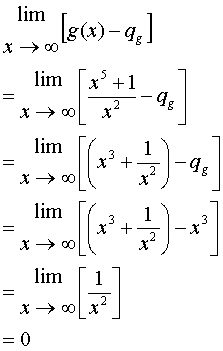
What this derivation tells us is, again, that as the x values get large g(x) approaches its quotient and only touches it (when the distance is exactly zero) when x tends to infinity. The previous results are similar for f(x).

Below are some graphs visually explaining the behavior. The asymptotes are the red curves and f(x) and g(x) are in black.