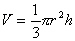
The volume of a cone is given below.
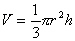
We wish for this to be a function of one variable so that we may employ Calculus to find a maximum. If you more accurately label the picture on the cone you will note a triangle. This triangle is formed by the radius of the cone r, the height of the cone h, and the length from the top down the side R. From this right triangle we can use the infamous Pythagorean theorem to deduce,
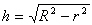 .
.So, we may now rewrite the original volume function with one variable.
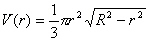
Before we proceed we should specify the domain of V. What values is r allowed to have. The smallest r can be is zero but how big can it be? Well, the only other variable which can be zero is h and i h=0 then r=R. So we have the domain of V(r) is [0,R]. Notice also that V(0)=0 and V(R)=0, so these will not give us a maximum (I hope) and the other possibility should come from Calculus methods. So, we now try to find critical points. We now take the derivative of V with respect to R and set it equal to zero.
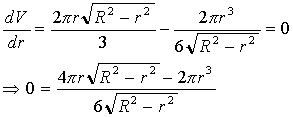
The critical points occur when either the numerator or denominator equal zero. Note that if the denominator equals zero then r=R which is the boundary condition from above and will give us no new information. So I will only concern myself with the numerator being zero. Indeed,
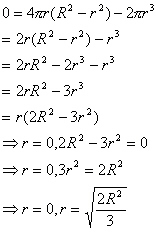
Since r=0 is the other boundary condition our only hope is that the other solution we have found gives us some positive volume. If so it will be the global maximum on our interval [0,R]. So we now evaluate the volume,
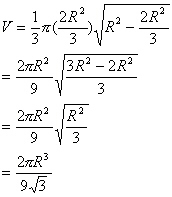
Thankfully, this value is a positive number and therefore it is our maximum volume and we are done.