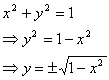
This is a really neat problem. It gives us insight into the fact that the shortest distance between a point and convex curve is found by dropping a perpendicular onto the curve from the point.

In order to begin this function we must have an idea of what equation to use. For the sake of brevity I will assume it to be clear that the shortest distance between the point (0,2) and the unit circle will be the distance of a straight line from (0,2) to the top half of the circle (as drawn in the picture). So we will need the equation for the top half of the circle. This can be found using the circle equation.

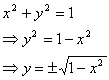
Where the positive square root is the top half of the circle and the negative square root is the bottom half. Next we need to find an equation governing the distance between the point (0,2) and the top half of the circle. For this we will employ the distance formula.

Now we will us the first derivative to find critical points.

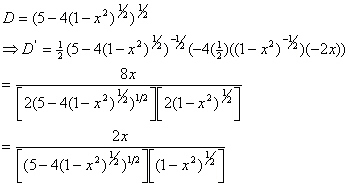
Grotesque as this derivative may be finding critical points can be broken down into two parts. When the numerator is zero or when the denominator is zero. If the numerator is zero then this implies that x=0 which is what we hope will be the value corresponding to the global minimum.

Setting each piece of the denominator equal to zero gives us the following.

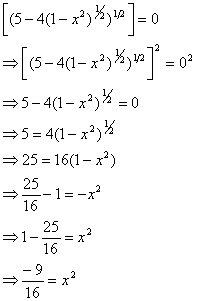
So, we have three points to check.

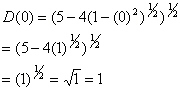
Since D(0)<D(1)=D(-1) and since the point on the top of the unit circle with an x-coordinate of zero is the point (0,1) we have completed the proof.